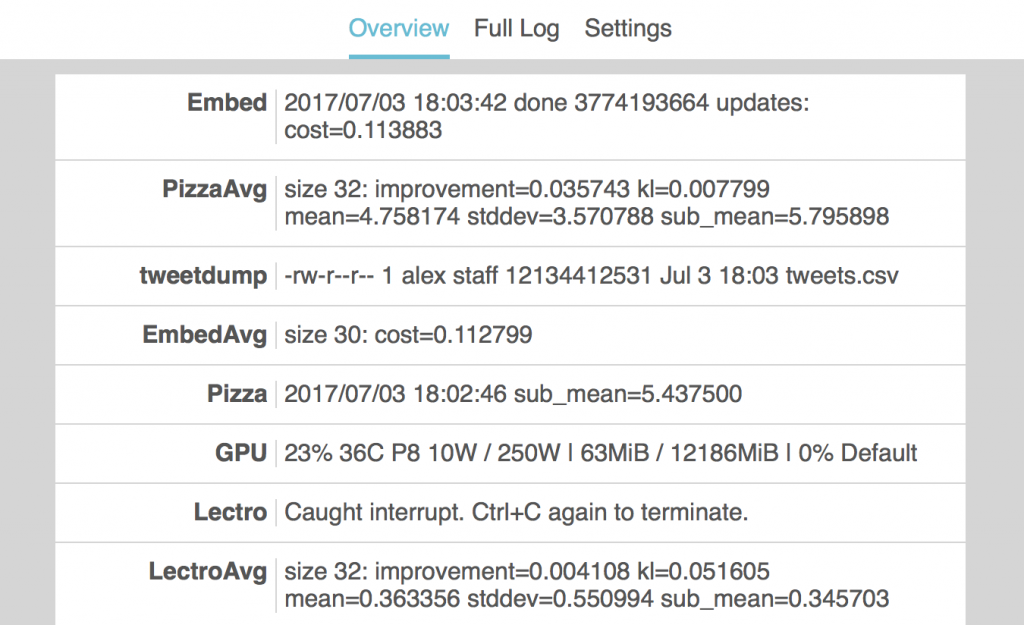
The MNIST dataset is split into 60K training images and 10K test images. Everyone pretty much assumes that the training images are enough to learn how to classify the test images, but this is not necessarily the case. So today, in the theme of being a contrarian, I’ll show you how to split the 70K MNIST images in an adversarial manner, such that models trained on the adversarial training set perform poorly on the adversarial test set.
Class imbalance is the most obvious way to make an adversarial split. If you put all the 2’s in the test set, then a model trained on the training set will miss all those 2’s. However, since this answer is fairly boring and doesn’t say very much, let’s assume for the rest of this post that we want class balance. In other words, we want the test set to contain 1K examples of each digit. This also means that, just by looking at the labels, you won’t be able to tell that the split is adversarial.
Here’s another idea: we can train a model on all 70K digits, then get the test set by picking the digits that have the worst loss. What we end up with is a test set that contains the “worst” 1K examples of each class. It turns out that this approach gives good results, even with fairly simple models.
When I tried the above idea with a small, single-layer MLP, the results were surprisingly good. The model, while extremely simple, gets 97% test accuracy on the standard MNIST split. On the adversarial split, however, it only gets 81% test accuracy. Additionally, if you actually look at the samples in the training set versus those in the test set, the difference is quite noticeable. The test set consists of a bunch of distorted, smudgy, or partially-drawn digits.
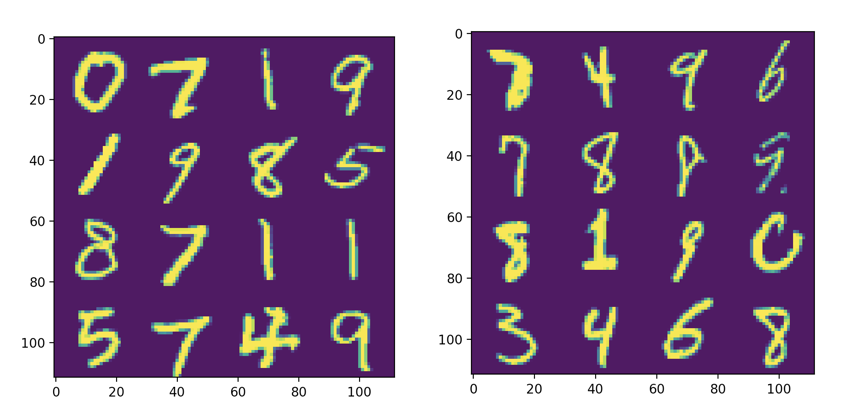
In a sense, the result I just described was obtained by cheating. I used a certain architecture to generate an adversarial split, and then I used the same architecture to test the effectiveness of that split. Perhaps I just made a split that’s hard for an MLP, but not hard in general. To truly demonstrate that the split is adversarial, I needed to test it on a different architecture. To this end, I tried a simple CNN that gets 99% accuracy on the standard test set. On the MLP-generated adversarial split, this model gets a whopping 87% test accuracy. So, it’s pretty clear that the adversarial split works across architectures.
There’s plenty of directions to take this from here. The following approaches could probably be used to generate even worse splits:
- Use an ensemble of architectures to select the adversarial test set.
- Use some kind of iterative process, continually making the split worse and worse.
- Try some kind of clustering algorithm to make a test set that is a fundamentally different distribution than the training set.
Maybe this result doesn’t mean anything, but I still think it’s cool. It shows that the way you choose a train/test split can matter. It also shows that, perhaps, MNIST is not as uniform as people think.
The code for all of this can be found here.